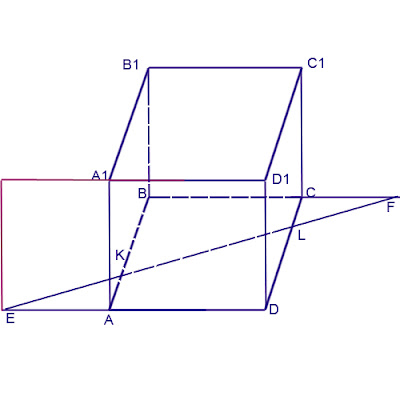
Дан куб ABCDA1B1C1D1 c ребром, равным a

Дан куб ABCDA1B1C1D1 c ребром, равным a. Точка K принадлежит ребру AB, точка L - ребру CD. При этом АК:КВ=1:3, CL:LD=1:4. Проведена прямая KL.

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

A1. Укажите точку пересечения прямой KL и плоскости A1D1D;
A2. Найдите точку пересечения прямых KL и BC;
A3. Укажите линию пересечения плоскостей ABC и B1EF

B1. Найдите длину отрезка B1K
B2. Вычислите длину отрезка KL

C1. Найдите длину отрезка EF

Решение:
А1.

Если продлим плоскость A1D1D то общей точкой пересечения будет точка Е

А2. F

А3.

KL линия пересечения плоскостей ABC и B1EF

B1. Проведем отрезок B1K

Из прямоугольного треугольника KBB1 найдем B1K

Сторона B1B=a
Сторона KB=3a/4 (сторона AB равна 4 частям, а KB составляет 3 части из 4)

По т.Пифагора

B1K^2=KB^2+BB1^2
B1K^2=(0,75a)^2+a^2
B1K^2=0,5625a^2+a^2
B1K^2=1,5625a^2
B1K=1,25a

B2. BCLK-прямоугольная трапеция

Проведем высоту LT=BC=a
BT=x
TK=3x-x=2x=0,5a (сторона AB равна 4 частям, а ТК составляет 2 части из 4)
Из прямоугольного треугольника TLK найдем LK

LK^2=TK^2+TL^2
LK^2=(0,5a)^2+a^2
LK^2=0,25a^2+a^2
LK^2=1,25a^2
LK=√5a/4

C1.