Решить систему уравнений
3y^2-2xy=10
y^2-3yx-2x^2=5
Решение:
Первое уравнение 3y^2-2xy=10
Второе уравнение y^2-3yx-2x^2=5
из первого уравнения выразим х
х=(3y^2-10)/2у
y^2-3y(3y^2-10)/2у-2((3y^2-10)/2у )^2=5
y^2-3(3y^2-10)/2-((3y^2-10)^2)/(2у^2 )=5 |*2у^2
2y^4-3y^2 (3y^2-10)- (3y^2-10)^2 =10y^2
2y^4-9y^4+30y^2- (9y^4-60y^2+100) =10y^2
2y^4-9y^4+30y^2- 9y^4+60y^2-100 -10y^2 =0
-16y^4+80y^2-100 =0 |: (-4)
4y^4-20y^2+25 =0
y^2=t,t≥0
4t^2-20t+25=0
D=b^2-4ac=400-400=0
t1=20/8=2.5
y^2=2,5
y1=√2,5 и y2=-√2,5
х1=((3*(√2,5)^2-10))/(2*√2,5)=(-2.5)/(2√2,5)=-√2,5/2
х2=((3*(-√2,5)^2-10))/(2*(-√2,5))=(-2.5)/(-2√2,5)=√2,5/2
Ответ: (-√2,5/2; √2,5) (√2,5/2; -√2,5)
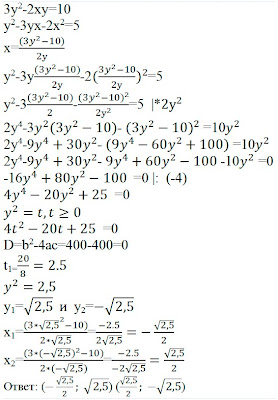
можно было просто второе уравнение умножить на два и потом приравнять
ОтветитьУдалитькак вариант решения можно ))
УдалитьДоброго времени суток, помогите решить систему уравнений (уровень С в экзаменах):
ОтветитьУдалить1{2x^2-3xy-y^2=4;
2{3x^2-2xy-2y^2=3;
Заранее спасибо за любые идеи и решения =)